X-Kette
Am folgenden Beispiel möchten wir Ihnen eine Situation erläutern, in der wir die Sudokustrategie der X-Kette anwenden).
Die schwarzen Zahlen sind die ursprünglich vorgegebenen. Die blauen Zahlen haben wir durch die Anwendung einfacher oder auch
schon fortgeschrittener Techniken gefunden. Die kleinen Zahlen stehen für die noch verbleibenden Möglichkeiten, es sind die so genannten
Kandidaten. (Im vorliegenden Beispiele können diese bereits durch den Einsatz anderer, fortgeschrittener Techniken weiter reduziert worden sein.)
Dieses Mal erläutern wir die Profi-Technik "X-Kette". Bei dieser Strategie spielt nur ein Kandidatenwert eine Rolle. Das Grundprinzip dabei ist, dass, wenn sich innerhalb einer Sudokueinheit
(Zeile, Spalte oder Block) genau zwei Kandidaten dieses bestimmten Werts befinden, genau einer davon die gesuchte Zahl sein muss, wogegen es der andere Kandidat logischerweise nicht ist
(Ausschlussprinzip). Lassen sich mehrere Einheiten finden, die jeweils zwei Kandidaten dieses Werts aufweisen und die sich überschneiden, entsteht eine Kette, in der die betroffenen Kandidaten
abwechselnd richtig oder falsch sind. Die logische Konsequenz ist nun die, dass sich in Bereichen, in denen sich sowohl ein falscher als auch ein richtiger Kandidat auswirken, kein anderer
Kandidat dieses Werts richtig sein kann.
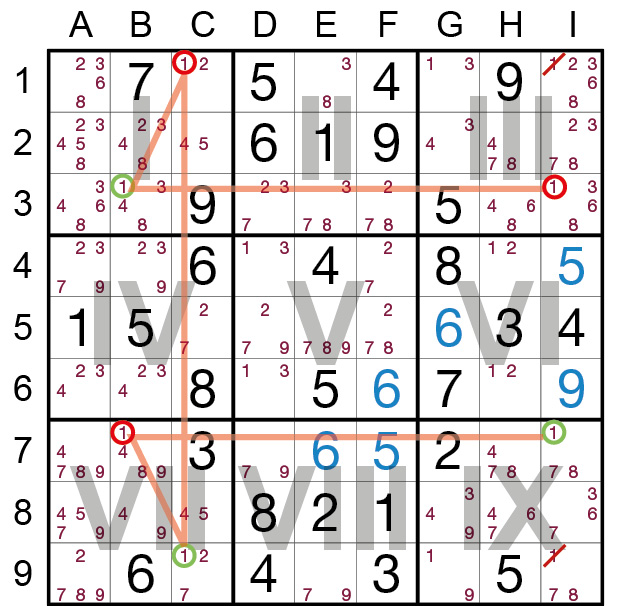
Was in allgemeiner Form beschrieben schwer fassbar klingt, ist in der Praxis einfach nachzuvollziehen – wie im Beispiel unten: Hier geht es um den Kandidatenwert 1 (im übertragenen Sinne ist es
somit eine "1-Kette"). Mehrere Einheiten enthalten diesen Wert jeweils genau zweimal. Die X-Kette, die wir damit bilden, haben wir grafisch hervorgehoben. Man kann leicht erkennen, dass entweder
die rot umkreisten 1en oder die grün umkreisten 1en richtig sein müssen. Probieren Sie es gedanklich aus: Entweder sind alle rot umkreisten 1en richtig, oder alle grün umkreisten 1en sind es. In
Spalte I entdecken wir sodann die mit dieser Technik bezweckte Möglichkeit, Kandidaten zu streichen: Dort nämlich sind sowohl eine "grüne" als auch eine "rote" 1 enthalten. Da wir nun wissen,
dass eine davon die richtige Zahl ist ("entweder alle rot umkreisten oder alle grün umkreisten"), können es die anderen 1en in dieser Einheit nicht sein und werden gestrichen.
Ein weitere Beispiel für die Anwendung einer X-Kette:
Gibt es in einer Einheit nur zwei Kandidaten eines Werts, so ist immer einer davon der richtige und der andere falsch. Findet man mehrere solcher Kandidatenpaare eines bestimmten Werts (hier: 3) und überschneiden sich deren Einheiten, so lassen sich logische Ketten bilden, in denen die Kandidaten abwechselnd wahr oder falsch sind. In den Feldern, die im Einflussbereich eines „wahren“ und eines „falschen“ Felds liegen, kann der Kandidat gestrichen werden.