X-Wing
Am folgenden Beispiel möchten wir Ihnen eine Situation erläutern, in der wir die Sudokustrategie des X-Wing anwenden.
Die schwarzen Zahlen sind die ursprünglich vorgegebenen. Die blauen Zahlen haben wir durch die Anwendung einfacher oder auch
schon fortgeschrittener Techniken gefunden. Die kleinen Zahlen stehen für die noch verbleibenden Möglichkeiten, es sind die so genannten
Kandidaten. (Im vorliegenden Beispiele können diese bereits durch den Einsatz anderer, fortgeschrittener Techniken weiter reduziert worden sein.)
Die Strategie, die wir in der unten dargestellten Situation anwenden, nennt sich X-Wing. Das logische Prinzip ist dabei folgendes: Taucht ein Kandidatenwert in zwei Zeilen (alternativ: Spalten)
in nur zwei Feldern auf und liegen diese je zwei Felder in denselben beiden Spalten (alternativ: Zeilen), können alle weiteren Kandidaten dieses Werts in diesen beiden Spalten (alternativ:
Zeilen) entfernt werden.
Warum das so ist, lässt sich anhand unseres konkreten Beispiels leichter nachvollziehen. In den Zeilen 4 und 9 (hier gelb) kommt der Kandidatenwert 2 nur jeweils zweimal vor (rot umkreist); einer
davon muss jeweils die gesuchte Zahl sein. Und da sich je zwei diese Kandidaten in derselben Spalte (hier: Spalten F und G) befinden, ergeben sich zwei Möglichkeiten: Entweder sind die beiden 2en
in den Feldern F4 und G9 die gesuchten Zahlen, oder die beiden 2en in G4 und F9 sind es. Unabhängig davon, welche dieser Möglichkeiten sich als richtig herausstellt, können wir folgern, dass in
den anderen Feldern dieser beiden Spalten (hier: hellviolett) keine 2 sein kann. Dort können wir die betroffenen Kandidaten also streichen.
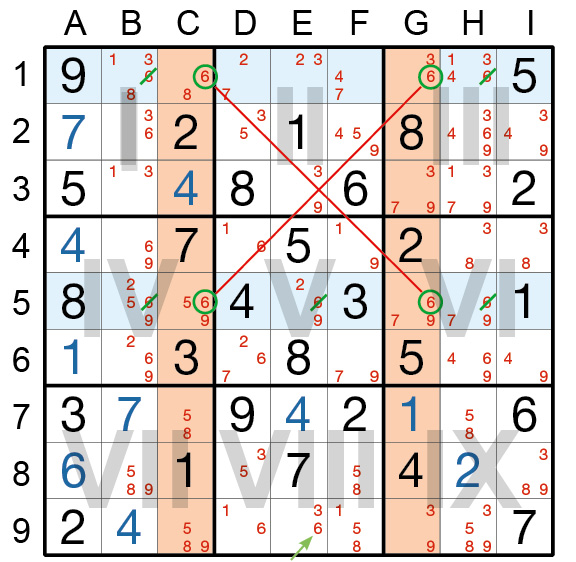
Auch im nächsten Beispiel können Sie versuchen, das logische Prinzip nachzuvollziehen. In den Spalten C und G (hier orange) kommt der Kandidatenwert 6 jeweils genau zweimal vor (grün umkreist);
einer davon muss jeweils die gesuchte Zahl sein. Und da sich je zwei dieser insgesamt vier Kandidaten in derselben Zeile (hier: Zeilen 1 und 5) befinden, ergeben sich zwei Möglichkeiten:
Entweder sind die beiden 6en in den Feldern C1 und G5 die gesuchten Zahlen, oder die beiden 6en in G1 und C5 sind es. Unabhängig davon, welche dieser Möglichkeiten sich als richtig herausstellt,
können wir folgern, dass in den anderen Feldern dieser beiden Zeilen (hier: hellblau) keine 6 sein kann. Dort können wir die betroffenen Kandidaten also streichen.
Der Einsatz hat sich gelohnt. Als Folge davon bleibt in Spalte E nurmehr ein Kandidat 6 übrig.
Weitere Beispiele für die Anwendung eines X-Wing:
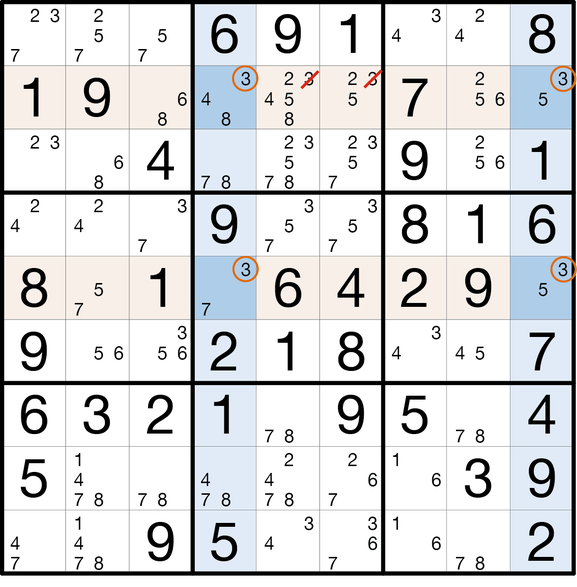
Existiert ein Kandidatenwert (hier: 3) in zwei Spalten (hier: S4 und S9) in jeweils nur zwei Feldern, und liegen diese vier Felder in nur zwei Zeilen (hier: Z2 und Z5), dann können alle weiteren Kandidaten dieses Werts aus diesen beiden Zeilen entfernt werden (da nur möglich: Z2S4 + Z5S9 ODER Z5S4 + Z2S9).